ECOGEN is a receptacle of a story of diffuse-interface-method (DIM) theory that started in the late 90s.
DIM summarizes more than 20 years of researches on multiphase flow1 modelling with the goal to develop mathematical models as well as their associated numerical methods.
What is a diffuse interface? In DIM theory, the interfaces between pure phases are captured as diffuse numerical regions, meaning that one goes continuously from one phase to another.
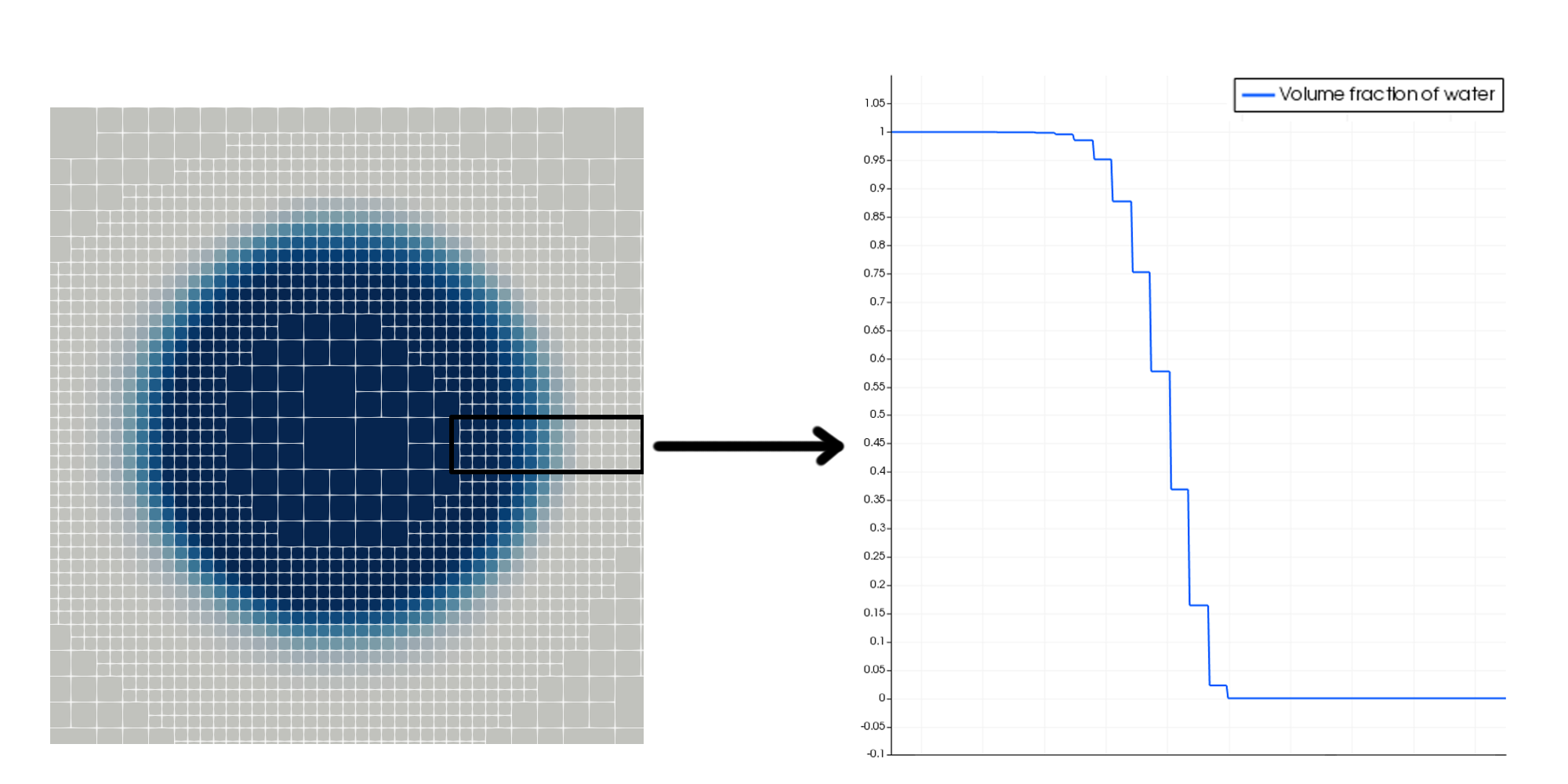1D extraction of the diffuse-interface region of a water droplet.
This way is possible thanks to a thermodynamics consistency. Then, the flow solution does no longer requires interface tracking algorithms: It becomes easy to simulate complex topological-shape evolutions between miscible or non-miscible fluids. Moreover, pressure waves (shock waves, acoustic waves) can propagate and interact properly in the whole flow.
The base research on DIM is now matured enough to propose ECOGEN, a numerical tool that can be largely cast and use to solve industrial as well as research multiphase flow problems. Hereafter are presented some recent applications involving different physical effects.
Physics of Shock
Shock waves can propagate in matter whatever its physical state: Gaseous, liquid or even solid. They can travel through interfaces or into a multiphase mixture of materials. Because ECOGEN is devoted to compressible, hyperbolic systems of equations, shock dynamics is included whatever the problem is.
Shock-wave propagation in ducts is a challenging problem for safety issues. Such studies are performed to improve the safety in confined installation thanks to a better knowledge of the pressure-wave characteristics. In this movie, the shock-wave propagation in a "Y" bifurcation channel is shown: Because of the bifurcation, the amplitude of the incident pressure jump is expected to decrease in the secondary ducts.
Shock-wave propagation in a channel junction (A. Marty courtesy).
Interaction shock wave / helium bubble
Upper half: Volume fraction
Lower half: Numerical schlieren (shows interfaces and shocks)
This video illustrates the shock/bubble interaction: The bubble contains lighter fluid (He) than the surrounding gas (air). Richtmyer-Meshkov instabilities deform the interface where the pressure and density gradients generate vorticity. Main parameters of the flow pattern are the acoustic impedance and so indirectly the speed of sound of both fluids.
Cavitation
The ability to treat cavitation problems is definitely one of the major assets of the diffuse-interface formulation. Now, thanks to consistent thermodynamics consideration, it is possible to intrinsically simulate interface appearance / disappearance between a liquid and its vapor without any specific algorithm for interface tracking.
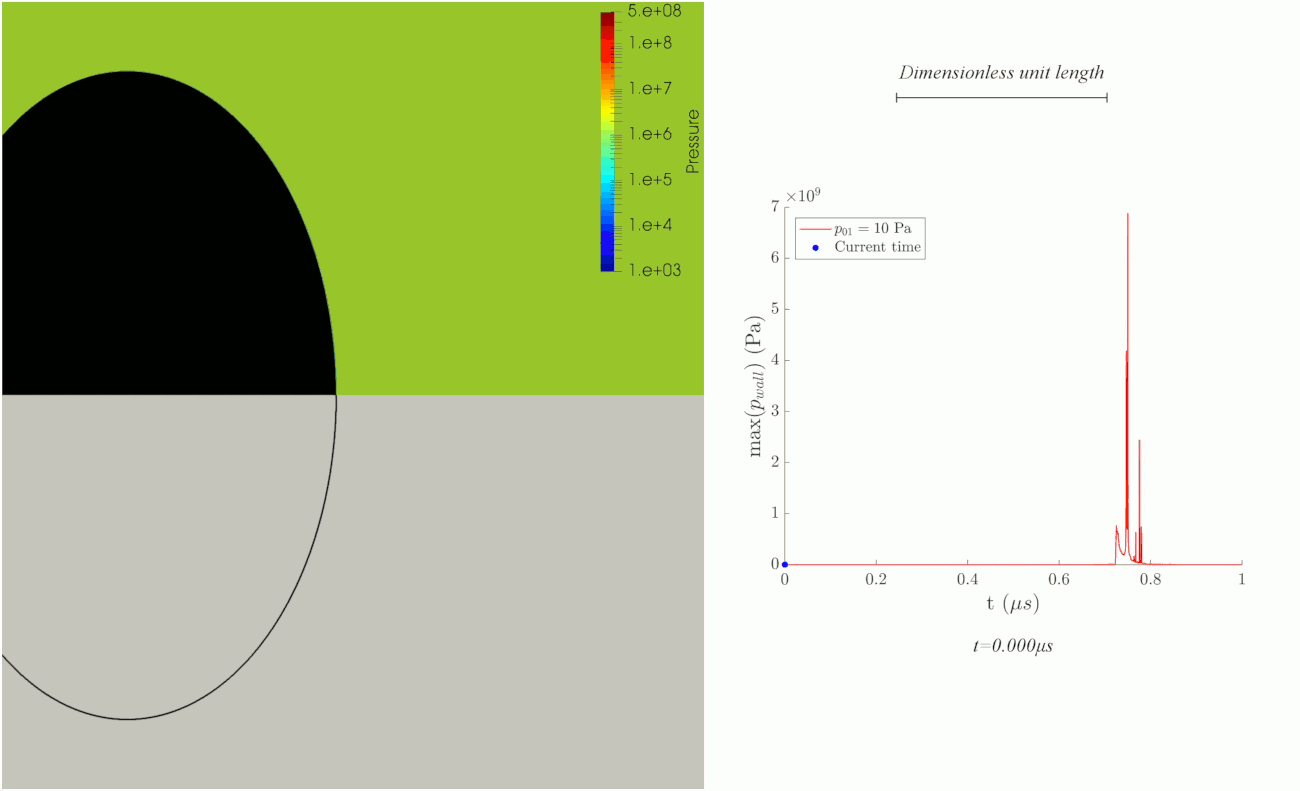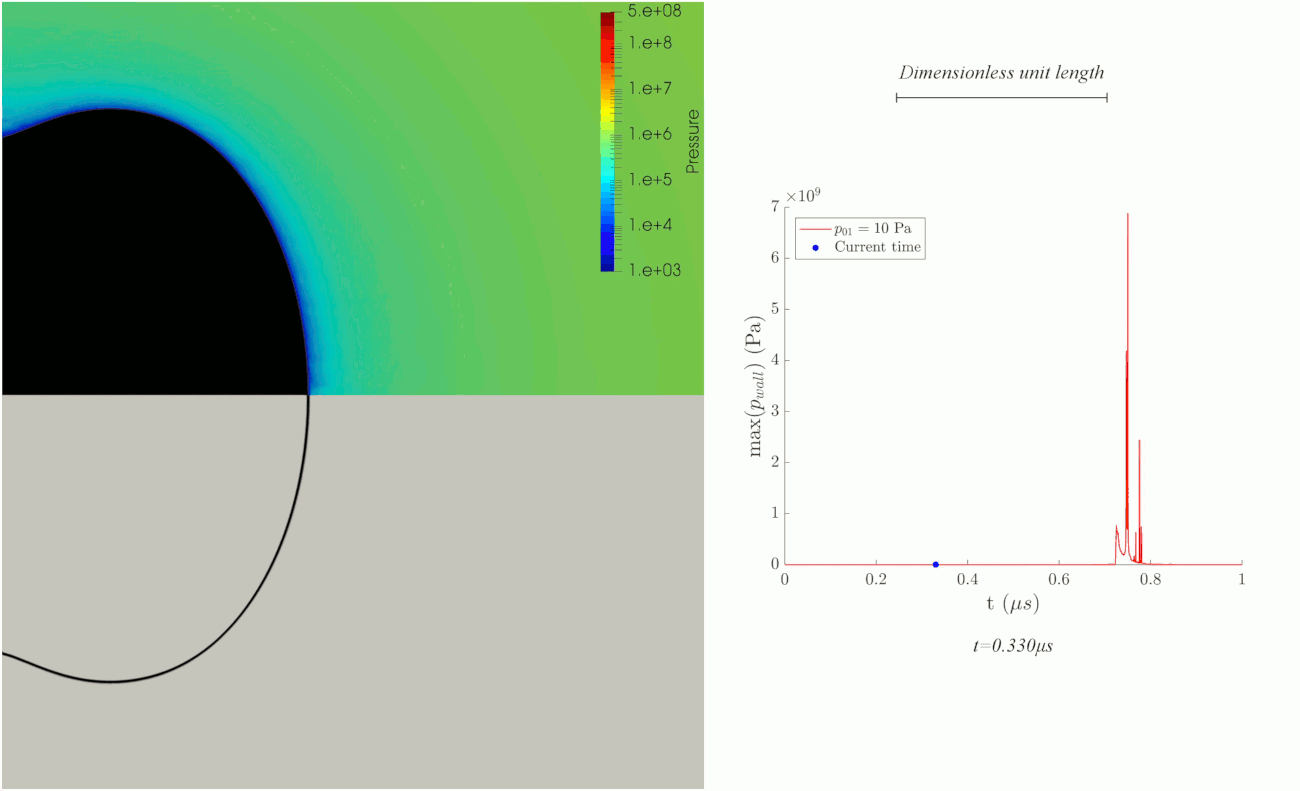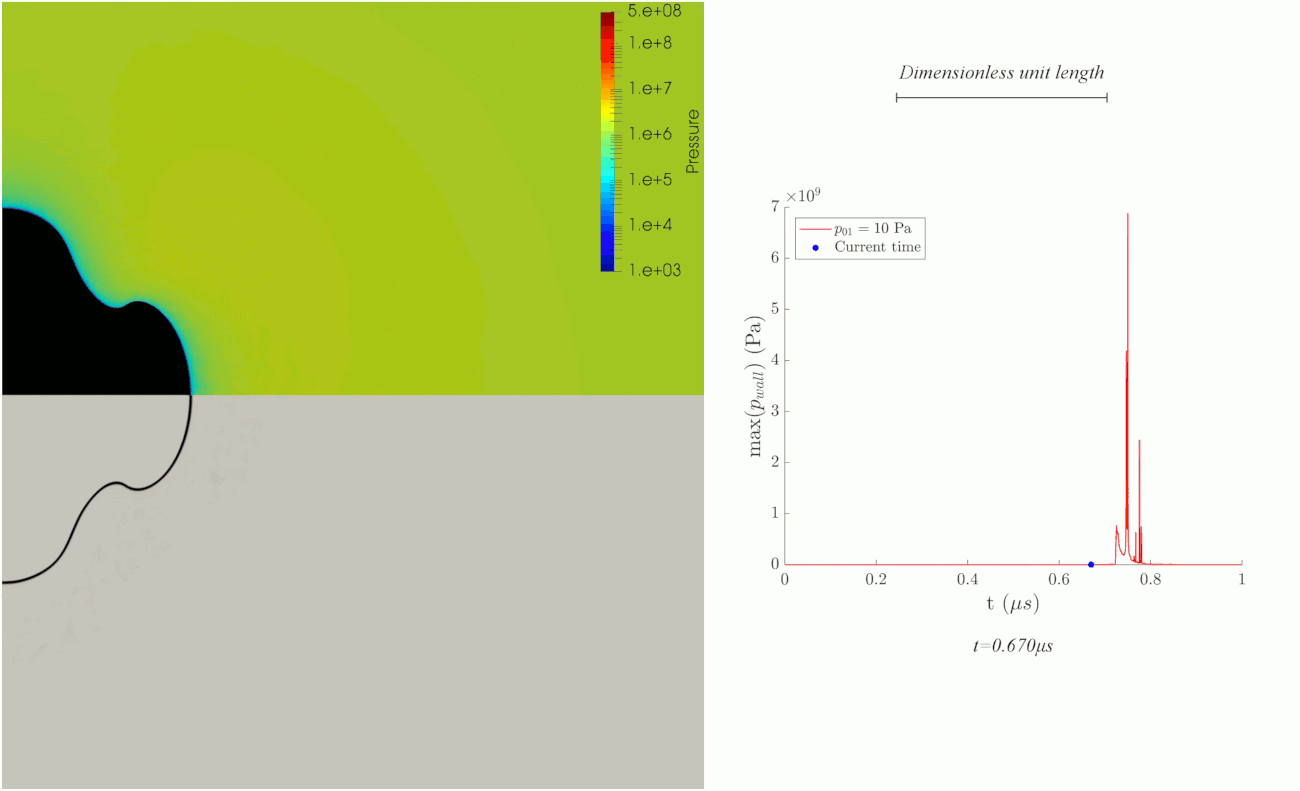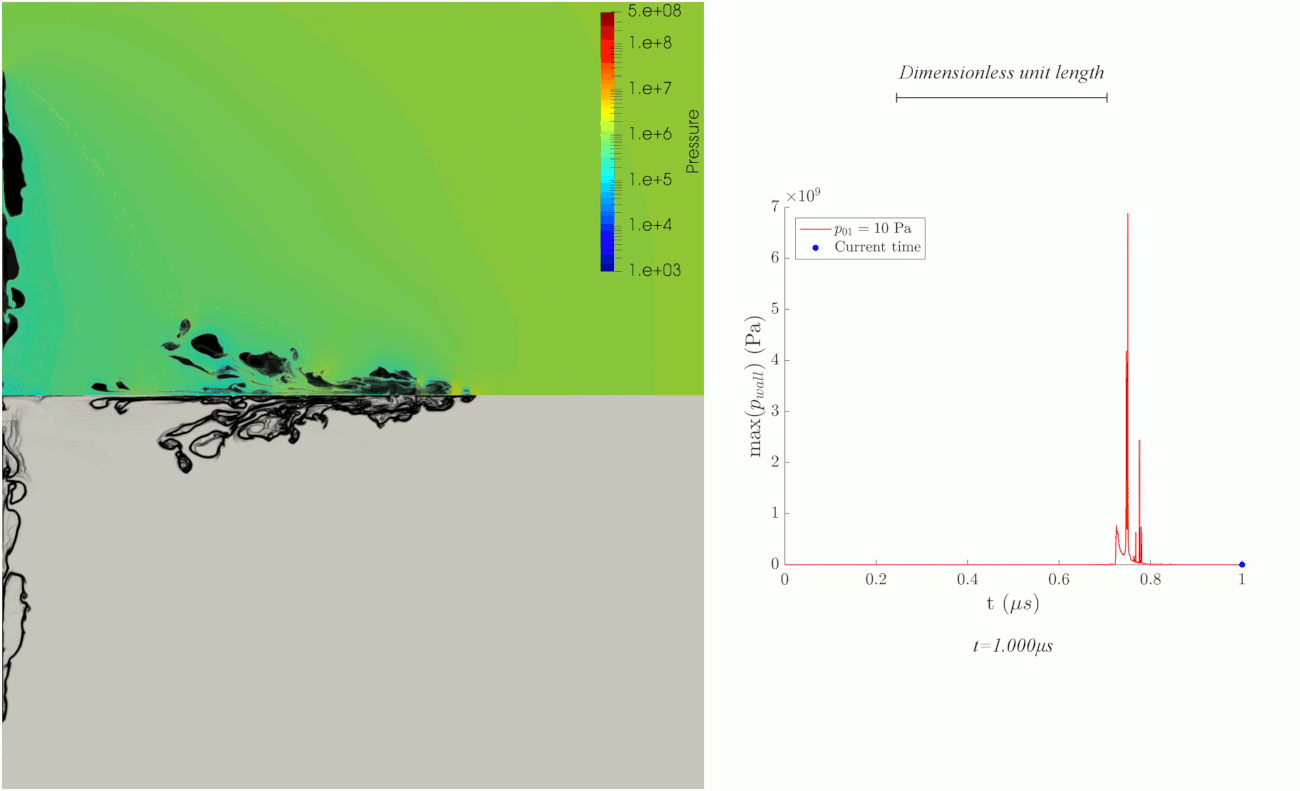Bubble collapse near a wall. Courtesy of Caltech, MCE.
Collapse of an ellipsoidal microbubble attached to a flat rigid surface for studying minimally invasive treatment of urinary stones. The simulation is 2D axisymmetric. Left panel shows pressure in color overlaid by the volume fraction of gas (upper half) and numerical schlieren of mixture-density gradients (lower half). Right panel shows maximum pressure at the rigid wall.
This very complex flow shows two major phenomena due to a high-speed bubble of water impacting a wall (on the left): A right-moving shock wave is created. One can then observe the typical interaction of a bubble that contains heavy fluid (water) in a lighter fluid (air) with Richtmyer-Meshkov instabilities. The impact on the wall also creates left-moving expansion waves leading to the appearance of cavitation pockets due to the decreasing pressure.
Water/air Richtmyer-Meshkov instability
Cavitation pockets on a three blades inducer.
In a rocket engine turbopump, the very high speed movement of the blades can lead to the formation of vapor structures.
In some critical cases, cavitation can then cause a decrease in the overall performance of the pump. In this picture, cavitation pockets appearing at the leading edge tips are captured using a thermodynamically consistent phase change approach.
Droplet fragmentation
The simulation of droplet fragmentation is of prime interest considering various industrial applications as well as for academic knowledge. The deformation of the droplet is a competition between surface tension and inertial forces (measured by the Weber number) that can lead to the creation of smaller droplets. Surface tension then determines the resulting droplet sizes.
Fragmentation of a droplet in a high-speed flow
The movie shows a water-droplet atomization by the high-speed flow produced by a shock wave at Mach 1.3. Contours, using water volume fraction equal to 10e-3 and mixture-velocity-norm colormap (dark red shows strong mixture-velocity norms and dark blue shows small ones), are shown to observe filaments and potential reduced-size droplets.
In this movie, a liquid droplet is moving in a box with perfect solid walls. At the impact on the upper wall, the bubble is sliding, deforming then dividing in smaller droplets. Due to the gravity, some small droplets fall down while a droplet is sliding down along the vertical wall. One can observe the rebounds of the droplets as well as the various droplet/droplet interactions leading to coalescence phenomena.
Motion and fragmentation of a liquid droplet in a box with solid walls.
Simulation including surface-tension effects and gravity.
